Conjuntos numéricos
N° Naturales:La exigencia y oportunidad de contar derivó necesariamente en la invención y el uso de los llamados actualmente números naturales. Aparecen en una gama de sistemas de numeración, en principio de carácter oral. Son los números más simples de los que hacemos uso, el conjunto de ellos se denota por . Entre estos números, en sucesión ascendente en representación indo-arábiga, son : 1,2,3,4,5... Se denominan también números enteros positivos.






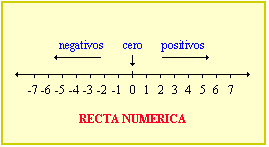
N° Enteros:La insuficiencia de los números naturales para contar deudas o temperaturas por debajo de cero lleva directamente a los números enteros. Se denotan por  y estan formados por los números naturales, sus inversos aditivos y el cero. El conjunto de los números enteros incluye a los naturales, .






N° Racionales:La insuficiencia de los números enteros para denominar partes de unidad lleva directamente a los números racionales. Se denotan por  y son todos aquellos que se pueden expresar de la forma  donde  y  son enteros y . Estos pueden ser enteros (en el caso en que ), decimales finitos o decimales infinitos periódicos. El conjunto de los números racionales incluye a los enteros, .





N° Irracionales:La insuficiencia de los racionales al intentar encontrar la medida exacta de la diagonal de un triángulo rectángulo con catetos de longitud 1 lleva a los números irracionales. Se denotan por A veces se denota por  al conjunto de los números irracionales. Esta notación no es universal y muchos matemáticos la rechazan. Las razones son que el conjunto de números irracionales no constituyen ninguna estructura algebraica, como sí lo son los naturales (), los enteros (), los racionales (), los reales () y los complejos (), por un lado, y que la  es tan apropiada para designar al conjunto de números irracionales como al conjunto de números imaginarios.



N° Reales:El conjunto de los números reales es la unión entre el conjunto de los números racionales y los irracionales.









N° cuadrados, triangulares, pentagonales y hexagonales

Función cuadrática

Una función cuadrática es aquella que puede escribirse como una ecuación de la forma:

f(x) = ax 2 + bx + c

donde a , b y c (llamados términos ) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero .

En la ecuación cuadrática cada uno de sus términos tiene un nombre.

Así,

ax 2 es el término cuadrático

bx es el término lineal

c es el término independiente

Cuando estudiamos la ecuación de segundo grado o cuadrática vimos que si la ecuación tiene todos los términos se dice que es una ecuación completa , si a la ecuación le falta el término lineal o el independiente se dice que la ecuación es incompleta .

Representación gráfica de una función cuadrática

Si pudiésemos representar en una gráfica "todos" los puntos [x,f(x)] de una función cuadrática , obtendríamos siempre una curva llamada parábola .

Parábola del puente, una función cuadrática.

Como contrapartida, diremos que una parábola es la representación gráfica de una función cuadrática .

Dicha parábola tendrá algunas características o elementos bien definidos dependiendo de los valores de la ecuación que la generan.

Estas características o elementos son:

Orientación o concavidad (ramas o brazos)

Puntos de corte con el eje de abscisas (raíces)

Punto de corte con el eje de ordenadas

Eje de simetría

Vértice

Orientación o concavidad

Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax 2 ) :

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x 2 − 3x − 5

Si  a < 0 (negativo) la parábola es convexa o con puntas hacia abajo, como en f(x) = −3x 2 + 2x + 3

Además, cuanto mayor sea |a| (el valor absoluto de a), más cerrada es la parábola.

Puntos de corte en el eje de las abscisas (Raíces o soluciones) (eje de las X)

Otra característica o elemento fundamental para graficar una función cuadrática la da el valor o los valores que adquiera x , los cuales deben calcularse.

Ahora, para calcular las raíces (soluciones) de cualquier función cuadrática calculamos

f (x) = 0 .

Esto significa que las raíces (soluciones) de una función cuadrática son aquellos valores  de x para los cuales la expresión vale 0; es decir, los valores de x tales que y = 0 ; que es lo mismo que f(x) = 0 .

Entonces hacemos

ax² + bx +c = 0

Como la ecuación ax² + bx +c = 0 posee un término de segundo grado, otro de primer grado y un término constante, no podemos aplicar las propiedades de las ecuaciones, entonces, para resolverla usamos la fórmula:

Entonces, las raíces o soluciones de la ecuación cuadrática nos indican los puntos de intersección de la parábola con el eje de las X (abscisas) .

Respecto a esta intersección, se pueden dar tres casos:

Que corte al eje X en dos puntos distintos

Que corte al eje X en un solo punto (es tangente al eje x)

Que no corte al eje X

Esta característica se puede determinar analizando el discriminante , ya visto en las ecuaciones cuadráticas .

Ver: Ecuaciones de segundo grado o cuadráticas

Ver: PSU: Matemática;

Pregunta 34_2010

Pregunta 18_2006

Punto de corte en el eje de las ordenadas (eje de las Y)

En el eje de ordenadas (Y) la primera coordenada es cero , por lo que el punto de corte en el eje de las ordenadas lo marca el valor de c (0, c) .

Veamos:

Representar la función f(x) = x² − 4x + 3

 

El eje de las ordenadas (Y) está cortado en +3

Representar la función f(x) = x² − 4x − 3

 

El eje de las ordenadas (Y) está cortado en −3

Observar que la parábola siempre cortará al eje de las ordenadas (Y), pero como ya vimos más arriba al eje de abscisas (X) puede que no lo corte, lo corte en dos puntos o solamente en uno.

Eje de simetría o simetría

Otra característica o elemento de la parábola es su eje de simetría .

El eje de simetría de una parábola es una recta vertical que divide simétricamente a la curva; es decir, intuitivamente la separa en dos partes congruentes. Se puede imaginar como un espejo que refleja la mitad de la parábola.

Su ecuación está dada por:

 

Donde x 1 y x 2 son las raíces de la ecuación de segundo grado en x , asociada a la parábola.

De aquí podemos establecer la ecuación del eje de simetría de la parábola:

Vértice

Como podemos ver en gráfico precedente, el vértice de la parábola es el punto de corte (o punto de intersección) del eje de simetría con la parábola y tiene como coordenadas

La abscisa de este punto corresponde al valor del eje de simetría  y la ordenada corresponde al valor máximo o mínimo de la función,  según sea la orientación de la parábola (recuerde el discriminante )

Función cuadrática

Como ya sabes, una función es una relación entre dos magnitudes, x y f(x), de manera que a cada valor de la primera magnitud le corresponde un único valor de la segunda, que se llama imagen. 

Función cuadrática es aquella función que está determinada por la ecuación de segundo grado (cuadrática) de la forma;

Donde a, b y c son números reales, y a ≠ 0, ya que si a = 0 se anula x², y no sería una ecuación cuadrática.

La representación gráfica de una función cuadrática se denomina parábola.

2- Representación gráfica: Parábola

La parábola de la función cuadrática, es una curva simétrica con respecto a una recta paralela al eje de las ordenadas, la cual se denomina eje de simetría. La parábola se compone de todos los pares ordenados (x, y) que satisfacen la ecuación cuadrática          y = ax² + bx c. 

El trazado de parábola de la función cuadrática está determinada por un vértice,  por el cual se traza el eje de simetría, lospuntos de corte en el eje x y el punto de corte en el eje y. Al trazado de la parábola se le denomina ramas de la parábola.

Si graficamos una parábola de una función cuadrática, podemos ver:

Estos puntos que forman la parábola, están determinados por los coeficientes numéricos a y b de x² y x respectivamente, y el término independiente c de la ecuación cuadrática.

2.1- Ramas de la parábola

Para determinar el sentido de las ramas de la parábola (hacia arriba o hacia abajo), dependerá del coeficiente numérico a dex².

Si a es mayor que cero (o sea, a es un número positivo), las ramas de la parábola irán hacia arriba, y si a es menor que cero (o sea, a es un número negativo), las ramas de la parábola irán hacia abajo.

También dependerá del  coeficiente numérico a, la dilatación o contracción de la parábola, ya que, si aumenta el valor absoluto de a, la parábola se contrae y si disminuye el valor absoluto de a, la parábola se dilata.

Veamos un ejemplo;

2.2- Punto de corte con el eje y

El punto de corte en el eje y está determinado por el valor del término independiente c, ya que, si analizamos una función cuadrática y = f (x) = ax² + bx + c, con x = 0 obtenemos;

Entonces, el punto de coordenadas (0, c)  de una función cuadrática f (x) = ax² + bx + c, corresponde al punto en que la parábola corta al eje y. 

2.3- Puntos de corte con el eje X

Para determinar los puntos donde la parábola atravesará el eje x o de las abscisas, analizaremos la función cuadrática y = f (x) = a^x2 + bx + c. Primero, sabemos que los puntos sobre el eje x tienen que tener coordenada y igual a cero (x, 0), por lo tanto la función es igual a cero y = f (x) = 0, que es igual a;  

Como puedes ver, tenemos una ecuación de segundo grado con una incógnita, la cual podemos resolver con la fórmula general;

Entonces, así obtenemos las dos raíces de la ecuación cuadrática, serían los puntos de intersección con el eje x. Las coordenadas de estos puntos serán;

Como sabemos, las raíces de una ecuación cuadrática dependen del discriminante.

Recuerda que el discriminante es la cantidad subradical b² - 4 a c y se designa con la letra delta.

Según el valor del discriminante, la función cuadrática corta dos, una o ninguna vez el eje x;

2.4- Vértice y eje de simetría

El vértice es el punto donde cambia de dirección la parábola, es por donde pasa el eje de simetría. Cuando a > 0 el vértice será el punto mínimo de la parábola, en cambio, sí   a < 0 el vértice será el punto máximo de la parábola.

Para encontrar el vértice, debemos obtener las coordenadas de este punto.

Para esto, sabemos que la parábola es simétrica, por lo tanto, podemos encontrar el componente x del vértice que se denomina x_v, ya que está justo en la mitad entre las raíces (o soluciones) de la ecuación cuadrática.

Entonces, el componente x_v, lo podemos encontrar promediando las raíces;

Según las propiedades de las raíces x₁ + x₂ = (- b/a). Reemplazamos;

Obteniendo este punto podemos trazar el eje de simetría, ya que, éste es una recta paralela al eje y (ordenadas) y que pasa por el vértice.

Luego, para encontrar el componente y, que se denomina y_v, reemplazamos x_v en la fórmula de función cuadrática;

Entonces, las coordenadas del vértice de una parábola de función cuadrática de la forma  f (x) = ax² + bx + c serán;

Si lo graficamos sería;

Si analizas estas coordenadas te darás cuenta que;

• Si b = 0, el eje y es el eje de simetría de la parábola.

• Si a > 0 y b > 0, el vértice de la parábola se encontrará a la izquierda del eje y, ya que;  - b/2a < 0.

• Si a > 0 y b < 0, el vértice de la parábola se encontrará a la derecha del eje y, ya que;  - b2a > 0.

• Si a < 0 y b < 0, el vértice de la parábola se encontrará a la izquierda del eje y, ya que; - b/2a < 0.

• Si a < 0 y b > 0, el vértice de la parábola se encontrará a la derecha del eje y, ya que;  - b2a > 0.

Ejemplos de funciones cuadráticas;

1) Grafiquemos la función y = x² + 1.

Para poder graficar esta función cuadrática debemos asignar arbitrariamente valores a x para encontrar los que corresponden a y. Luego de hacer esta tabla podrás graficar en el plano cartesiano. 

En la parábola de esta función podemos observar que;

- La curva no toca el eje x, por que las raíces son imaginarias.

Esto lo que podemos comprobar si reemplazamos b² - 4ac = 0² - 4 = - 4. Como la discriminante es negativa la curva no toca el eje x.

- La parábola está hacia arriba ya que a = 1, o sea, a > 0.

- El vértice es (0,1) para esta función como a > 0 es el punto mínimo de la parábola, y el eje de simetría corresponde al eje de las ordenadas.

- El eje y se corta en el mismo punto del vértice, ya que c = 1.

2) Grafiquemos la función y = - x² + 2x + 8.

Igual como en el ejemplo 1 asignamos valores a x para encontrar los que corresponden a y, luego graficamos.

En la parábola de esta función podemos observar que;

- La curva toca al eje x en dos puntos cuyas coordenadas son (-2,0) y (4,0).  Recuerda que los puntos donde la parábola corta el eje x son las raíces de la ecuación cuadrática.

Además podemos comprobar que la parábola corta al eje x en dos puntos, ya que, si reemplazamos los datos en la discriminante b² - 4ac = 4 + 32 = 36. Como la discriminante es positiva la curva corta al eje x en dos puntos.

- La parábola está hacia abajo ya que a = -1, o sea, a < 0.

- El vértice es (1,9) para esta función como a < 0 es el punto máximo de la parábola. Lo puedes verificar ocupando las fórmulas para encontrar el vértice (- b/2a, c – b²/4a).

- El eje y se corta en el punto (0,8), ya que c = 8.

Funciones exponenciales

Las funciones exponenciales son las funciones que tienen la variable independiente   x   en el exponente, es decir, son de la forma:

Las características generales de las funciones exponenciales son:

1) El dominio de una función exponencial es R.

2) Su recorrido es   (0, +∞) .

3) Son funciones continuas.

4) Como   a⁰ = 1 , la función siempre pasa por el punto   (0, 1).

    La función corta el eje Y en el punto   (0, 1)   y no corta el eje X.

5) Como   a¹ = a , la función siempre pasa por el punto   (1, a).

6) Si   a > 1   la función es creciente.

    Si   0 < a < 1   la función es decreciente.

7) Son siempre concavas.

8) El eje X es una asíntota horizontal.

• Si a > 1 :
  
  Al elevar un número mayor que  1  a cantidades negativas cada vez más grandes, el valor de la potencia se acerca a cero, por tanto : 
  
  Cuando  x → - ∞ , entonces  a ^x → 0


• Si 0 < a < 1 :
  
  Ocurre lo contrario que en el caso anterior :
  
  Cuando  x → + ∞ , encontes  a ^x → 0

Ejemplo de funciones exponenciales: 

1) Dominio:

El dominio de las funciones exponenciales es R.

Dom(f) = Dom(g) = R .

2) Recorrido:

El recorrido de las funciones exponenciales es   (0, + ∞) .

Im(f) = Im(g) = (0, + ∞) .

3) Puntos de corte:

f(0) = 2⁰ = 1  , el punto de corte con el eje Y es  (0, 1).

g(0) = - 2⁰ = 1  , el punto de corte con el eje Y es  (0, 1).

La funciones   f(x)   y   g(x)   no cortan al eje X.

4) Crecimiento y decrecimiento:

La función   f(x)   es creciente ya que   a > 1 .

La función   g(x)   es decreciente ya que   0 < a < 1 .

5) Concavidad y convexidad:

Las funciones   f(x)   y   g(x)   son concavas.

6) Asíntotas:

Las funciones   f(x)   y   g(x)   tienen una asintota en el eje X.

7) Tabla de valores:

Resumen de las propiedades de la función exponencial   e^x

1	La función exponencial es la inversa de la logarítmica:      y = ex      ⇔      x = Ln y
2	La función   y = ex  tiene por dominio   R   y por recorrido   y > 0
3	La función    y = ex  es continua, creciente e inyectiva en todo su dominio.
4	La función   y = ex   es cóncava hacia arriba en todo su dominio.
5

Ejemplo de funciones exponenciales:   f(x) = e^x

1) Dominio:

El dominio de las funciones exponenciales es R.

Dom(f) = R .

2) Recorrido:

El recorrido de las funciones exponenciales es   (0, + ∞) .

Im(f) = (0, + ∞) .

3) Puntos de corte:

f(0) = e⁰ = 1  , el punto de corte con el eje Y es  (0, 1).

La función   f(x)  no corta al eje X.

4) Crecimiento y decrecimiento:

La función   f(x)   es creciente ya que   e > 1 .

5) Concavidad y convexidad:

Las función   f(x)   es concava.

6) Asíntotas:

Las función   f(x)   tiene una asintota en el eje X.

7) Tabla de valores:

   Funciones polinómicas:

Las funciones polinómicas son, como su nombre lo dice, funciones que constan de un polinomio.

en donde n es un entero positivo, llamado, grado del polinomio. Resulta evidente, que el coeficiente del grado mayor, no puede ser cero, o sea, a tiene que ser diferente de cero, para que el grado del polinomio se n. Cualquiera de los otros coeficientes puede ser cero.
Ejemplos de funciones polinómicas son:
 , la cual es de grado 3, ya que el exponente mayor es 3.
, que es una función polinómica de grado 2, o sea cuadrática, cuya gráfica es una parábola.
, que es de grado 6, ya que multiplicando todos los paréntesis, nos daría como mayor exponente el 6. Esta función se grafica más adelante, para hacer notar, que las intersecciones con los ejes y la factorización de la función polinomial tienen una estrecha relación.
La gráfica de las funciones polinómicas depende del grado de la función. Las funciones polinómicas de ciertos grados tienen ciertas alternativas de gráfica. Queda a este curso de derivadas averiguar algunas de las características de las funciones para poder predecir su comportamiento.
Muchas veces a partir de la gráfica de un polinomio se puede deducir la ecuación de la función. Ésto se puede hacer a partir de las intersecciones con los ejes. (Conste que comenté, que muchas veces, NO SIEMPRE).
Una función polinómica con el más alto número de intersecciones con el eje "x" permisible, es aquella que se puede determinar su gráfica y su ecuación.
Una función de, por ejemplo, tercer grado puede tener como máximo 3 intersecciones con el eje "x".
Una función de sexto grado puede tener como máximo 6 intersecciones con el eje "x".
Cabe aclarar, que las funciones polinómicas, aunque no conozcamos ahora los términos específcos, son funciones continuas,sin asíntotas verticales, ni horizontales, que según el grado pueden presentar máximos, mínimos y puntos de inflexión.

Suponiendo que la función que se nos presenta es de tercer grado, y sus intersecciones están en x = 2, x = -1 y en x = -3; la ecuación de la función es f(x) = (x-2)(x+1)(x+3)

Debe quedar claro, que se tiene que conocer el grado de la función polinómica, ya que sin éste, las conclusiones que se puedan sacar pueden estas equivocadas. Tenemos una función polinómica de grado 6, que sus intersecciones se encuentran en x = 1, x = 2, x = -1, x = 3, x = -2 y en x = 0; por lo tanto la función es: f(x) = (x-1)(x-2)(x+1)(x-3)(x+2)(x)

FUNCION RACIONAL

Una función racional está definida como el cociente de polinomios en los cuales el denominador tiene un grado de por lo menos 1. En otras palabras, debe haber una variable en el denominador.

La forma general de una función racional es  , donde p ( x ) y q ( x ) son polinomios y q ( x ) ≠ 0.

Ejemplos: 

La función padre de una función racional es  y la gráfica es una hipérbola .

El dominio y rango es el conjunto de todos los números reales excepto 0.

Valor excluído  

En una función racional, un valor excluído es cualquier valor de x que hace al valor de la función y no definido. Así, estos valores deben ser excluídos del dominio de la función.

Por ejemplo, el valor excluído de la función  es –3. Esto es, cuando x = –3, el valor de y no esta definido.

Así, el dominio de esta función es el conjunto de todos los números reales excepto –3.

Asíntotas

Una asíntota es una recta que se acerca a la gráfica de la función, pero nunca la toca. En la función padre  , tanto los ejes x y yson asíntotas. La gráfica de la función padre se acercará más y más pero nunca tocará las asíntotas.

Una función racional de la forma  tiene una asíntota vertical en el valor excluído, o x = b , y una asíntota horizontal en y = c .

TRIGONOMETRIA

La trigonometría es la rama de las matemáticas que estudia la relación entre los lados y ángulos de los triángulos. Se ocupa, por tanto, de las funciones asociadas a los ángulos, denominadas funciones trigonométricas (también pueden denominarsefunciones circulares): seno, coseno, tangente, secante,…

Etimológicamente, trigonometría significa medida de los triángulos, ya que proviene de las palabras griegas trigono (triángulo) y metría (medida).

La trigonometría tiene innumerables aplicaciones en diversos campos de la ciencia: de una u otra manera en todos los campos de las matemáticas; en la física, por ejemplo en fenómenos ondulatorios; en la astronomía, por ejemplo para medir distancias entre planetas; en la geodesia, etc.

PROBABILIDAD